Flashcards: ideal properties, true RNG properties, PRNG properties, linear congruential generators and their types?
Properties of an ideal RNG:
- Repeatability: given the same starting point (seed) will generate the same sequence of random numbers - useful for testing.
- Long Cycle Length: stays random for very long sequences of numbers before repeating or becoming predictable.
- High Speed: can generate numbers very quickly.
There are two main types of RNG to fit this ideal:
- True RNG: useful for high-security systems where unpredictability is required; generated with unpredictable physical processes, like quantum phenomena or radioactive decay. These have no seeds, though, so are inherently not repeatable.
- Pseudo-RNG (PRNG or Computational RNG): useful for scientific computing, as they’re repeatable, portable (between programming languages), and closely approximate the statistical properties of uniformity and independence. Basically not truly random, but random enough.
- If it was a perfect PRNG, there would be the same count of each number within an interval - a uniform distribution.
Computer systems often come with a PRNG - fast, but could have short cycle lengths and have strong correlation patterns.
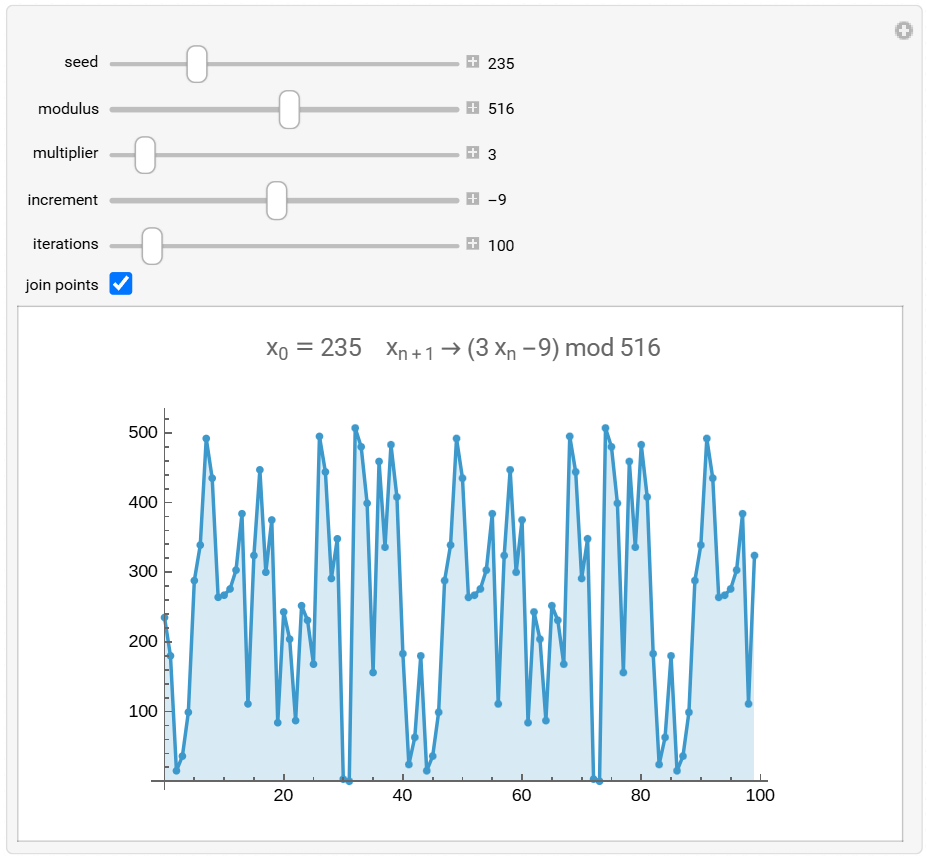
For example, the frequently used Linear Congruential Generators. This generates a sequence with the following recurrence relation:
The period of the sequence is at most , but can be shorter depending on the other constants, including the seed .
If , mixed congruential method, otherwise multiplicative.
Useful demo here: https://demonstrations.wolfram.com/LinearCongruentialGenerators.
Many useful sets of parameters have been found for this PRNGs, for example Numerical Recipes recommends .
I wonder how these were found?
Main differences between these two PRNGs?
#include <iostream>
#include <cstdlib> // Needed for rand() and srand()
#include <ctime> // Needed for time()
using namespace std;
int main()
{
int b, c;
double num[10]; // Declaration of the array for 10 numbers
double a;
int size;
size = 10; // Number of elements to sort out
// Seed the random number generator with the current time
//srand(static_cast<unsigned int>(time(0)));
// Initialization of the array
for (c = 0; c < size; c++)
// Random function with range [0,99]
num[c] = ((double)rand() / RAND_MAX )*100;
// Random function with range [-0.5, 0.5]
//num[c] = ((double)rand() / RAND_MAX) - 0.5;
// Displaying the array on the screen
cout << "Original numbers are: " << endl;
for (c = 0; c < size; c++)
cout << num[c] << endl;
cout << endl;
return 0;
}and
#include <iostream>
#include <cstdlib> // Needed for rand() and srand()
#include <ctime> // Needed for time()
using namespace std;
int main()
{
int b, c;
double num[10]; // Declaration of the array for 10 numbers
double a;
int size;
size = 10; // Number of elements to sort out
// Seed the random number generator with the current time
//srand(static_cast<unsigned int>(time(0)));
// Initialization of the array
for (c = 0; c < size; c++)
// Random function with range [0, 99]
//num[c] = (rand() % 100);
// Random function with range [1, 100
num[c] = (rand() % 100) +1;
// Displaying the array on the screen
cout << "Original numbers are: " << endl;
for (c = 0; c < size; c++)
cout << num[c] << endl;
cout << endl;
return 0;
}Differences: Between how they initialise arrays…
rand1.cpphandles floating-point numbers over , whilstrand2.cpphandles integers over .
A more modern RNG would first #include <random> and then have something like…
random_device rd; // Random device for seeding
mt19937 gen(rd()); // Mersenne Twister engine
uniform_real_distribution<double> dist(0.0, 1.0); // Uniform distribution in [0.0, 1.0)
// Initialization of the array with random numbers between 0 and 1
for (c = 0; c < size; c++) {
num[c] = dist(gen); // Generate random doubles in [0.0, 1.0)
}LAB TASKS:
Task 1.1: Write a C++ function to generate random numbers using the mixed linear congruential generator algorithm, i.e. follows…
/**
* @brief Generate random numbers using a mixed linear congruential generator.
*
* @details Generates random numbers using the formula:
* \f[
* X_{n+1} = (a \times X_n + c) \mod m
* \f]
* where \f$X_n\f$ is the previous random number, \f$X_{n+1}\f$ is the next random number,
* \f$a\f$ is the multiplier, \f$c\f$ is the increment, and \f$m\f$ is the modulus.
*
* @note Designed to experiment with random number generation using a mixed linear congruential
* generator.
*
* @param seed The initial seed value for the random number generator.
* @param multiplier The multiplier for the random number generator.
* @param increment The increment for the random number generator.
* @param modulus The modulus for the random number generator.
* @param count The number of random numbers to generate.
*
* @throw std::invalid_argument Throws an error if the multiplier, increment, or modulus are less
* than or equal to 0.
*
* @example
* \code{.cpp}
* generate_random_numbers(1, 5, 3, 16, 5);
* \endcode
*
* Expected Output:
* \code{.plaintext}
* Random Numbers:
* 1: 8
* 2: 11
* 3: 14
* 4: 1
* 5: 4
* \endcode
*/
void generate_random_numbers(int seed, int multiplier, int increment, int modulus, int count) {
/* Throw an error if the multiplier, increment, or modulus are less than or equal to 0. */
if (multiplier <= 0 || increment <= 0 || modulus <= 0) {
throw std::invalid_argument("Error: multiplier, increment, and modulus "
"must be greater than 0!");
}
/* Initialise the random number generator with the seed value. */
int random_number = seed;
/* Output the random numbers to the console. */
std::cout << "Random Numbers:" << std::endl;
for (int i = 1; i <= count; i++) {
/* Calculate the next random number with the mixed linear congruential generator formula. */
random_number = (multiplier * random_number + increment) % modulus;
/* Output the random number to the console. */
std::cout << std::setw(2) << i << ": " << random_number << std::endl;
}
}Task 1.2: Write a C++ program to extract six different random numbers (using the previously developed algorithm) in the interval and print the lucky numbers on screen. To extend this, evaluate the number of extractions required to win with matching numbers out of , given an arbitrary selection.
/**
* @file l01-randomness-generator.cpp
* @author William Fayers ([email protected])
* @brief Bingo game simulation using a mixed linear congruential generator
* @version 0.2.0
* @date 2025-01-26
*
* @copyright Copyright (c) 2025
*
*/
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include <stdexcept>
#include <ctime>
#include <algorithm>
#include <thread>
#include <chrono>
/**
* @brief Generate random numbers using a mixed linear congruential generator.
*
* @details Generates random numbers using the formula:
* \f[
* X_{n+1} = (a \times X_n + c) \mod m
* \f]
* where \f$X_n\f$ is the previous random number, \f$X_{n+1}\f$ is the next random number,
* \f$a\f$ is the multiplier, \f$c\f$ is the increment, and \f$m\f$ is the modulus.
*
* @note Results are adjusted to produce numbers in the 1-modulus range
*
* @param seed The initial seed value for the random number generator
* @param multiplier The multiplier for the random number generator
* @param increment The increment for the random number generator
* @param modulus The modulus for the random number generator
* @param count The number of random numbers to generate
*
* @throw std::invalid_argument Throws an error if the multiplier, increment, or modulus are less
* than or equal to 0.
*
* @return std::vector<int> A vector containing the generated random numbers
*/
std::vector<int> generate_random_numbers(
int seed,
int multiplier,
int increment,
int modulus,
int count)
{
if (multiplier <= 0 || increment <= 0 || modulus <= 0)
{
throw std::invalid_argument("Error: multiplier, increment, and modulus "
"must be greater than 0!");
}
int current_number = seed;
std::vector<int> numbers;
for (int iteration = 1; iteration <= count; iteration++)
{
current_number = (multiplier * current_number + increment) % modulus;
numbers.push_back(current_number + 1); // Adjust to 1-modulus range
}
return numbers;
}
/**
* @brief Main function for the bingo game simulation program
*
* @details Provides interactive bingo game experience where users can:
* 1. Choose how many numbers to guess (1-6)
* 2. Enter their unique guesses
* 3. See their calculated probability of winning
* 4. Experience a dramatic reveal of the bingo numbers
*
* @return int Returns 0 if the program exits successfully
*/
int main()
{
// Generate 6 unique bingo numbers using current time as seed
const int NUM_BINGO_NUMBERS = 6;
const int NUMBER_RANGE = 50;
std::vector<int> bingo_numbers = generate_random_numbers(
static_cast<int>(time(0)), // Seed with current time
5, // Multiplier
3, // Increment
NUMBER_RANGE, // Modulus (numbers will be 1-50)
NUM_BINGO_NUMBERS // Number of numbers to generate
);
// Get valid guess count from user
int guess_count;
do
{
std::cout << "How many numbers do you want to guess (1-" << NUM_BINGO_NUMBERS << ")? ";
std::cin >> guess_count;
if (guess_count < 1 || guess_count > NUM_BINGO_NUMBERS) {
std::cout << "Please enter a number between 1 and " << NUM_BINGO_NUMBERS << ", "
"with no repeats!\n";
}
} while (guess_count < 1 || guess_count > NUM_BINGO_NUMBERS);
// Collect valid user guesses
std::vector<int> user_guesses;
std::cout << "Enter your " << guess_count
<< " unique numbers between 1 and " << NUMBER_RANGE << ":\n";
for (int input_iteration = 0; input_iteration < guess_count; input_iteration++) {
int current_guess;
std::cin >> current_guess;
// Validate input range and uniqueness
while (current_guess < 1 || current_guess > NUMBER_RANGE ||
std::find(user_guesses.begin(), user_guesses.end(), current_guess)
!= user_guesses.end())
{
std::cout << "Invalid input. Enter a unique number between 1 and "
<< NUMBER_RANGE << ": ";
std::cin >> current_guess;
}
user_guesses.push_back(current_guess);
}
// Calculate probability using combinatorial mathematics
double win_probability = 1.0;
for (int probability_iteration = 0;
probability_iteration < guess_count;
probability_iteration++)
{
win_probability *= static_cast<double>(NUM_BINGO_NUMBERS - probability_iteration)
/ (NUMBER_RANGE - probability_iteration);
}
std::cout << std::fixed << std::setprecision(10);
std::cout << "\nYour chance of winning is: " << win_probability * 100 << "%\n";
// Check if all guesses match bingo numbers
bool has_won = true;
for (int user_guess : user_guesses)
{
if (std::find(bingo_numbers.begin(), bingo_numbers.end(), user_guess)
== bingo_numbers.end())
{
has_won = false;
break;
}
}
// Dramatic number reveal with delay
std::cout << "\nDrum roll...\nThe Bingo Numbers are: \n";
for (int bingo_number : bingo_numbers)
{
std::cout << std::setw(2) << bingo_number << " ";
std::cout.flush(); // Ensure immediate output
std::this_thread::sleep_for(std::chrono::milliseconds(500)); // Dramatic pause
}
std::cout << "\n\n";
// Final result announcement
if (has_won)
{
std::cout << "!!! WINNER WINNER CHICKEN DINNER !!! All your numbers are there!\n";
} else {
std::cout << "Sorry, no luck this time. Better luck next time!\n";
}
return 0;
}