Lagrangian and Hamiltonian Mechanics Coursework

Problem 1 (50 total marks)

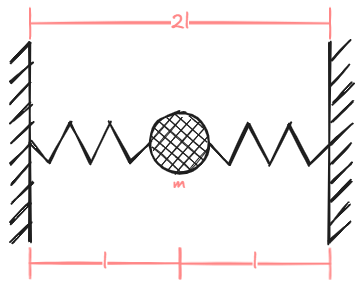
A point particle of mass $m$ is suspended horizontally on two springs of rest length $l$ between two solid walls, a distance of $2l$ apart. The spring constant of the left spring is $k$ and the right spring is $99k$.

This model is depicted below:

Part A (4 marks)

We can find the degrees of freedom of the particle by definition:

$$\text{d.f.}=kN-p$$

where $k$ is the number of dimensions, $N$ the number of particles, and $p$ the number of holonomic constraints. In this model, there is one particle ($N=1$) moving horizontally ($k=1$) without any holonomic constraints ($p=1$); since the only attachments to the particle are springs, which can be theoretically stretched infinitely and thus aren’t holonomic constraints. Hence,

$$\text{d.f.}=1\cdot 1-0=\boxed{1}$$

Part B (12 marks)

If we place the origin of the coordinate system at the midpoint between the walls, then $x$ is the horizontal displacement of the particle from this midpoint, such that the left wall is at $x=-l$, the right wall at $x=l$, and the point particle’s equilibrium at $x=0$.

From this, we can find the Lagrangian using its definition $L=T-U$, where $T$ is the kinetic energy $T=\frac{1}{2}m{\dot{x}}^2$ and $U$ is the potential energy $U=\frac{1}{2}k(l+x{)}^2+\frac{1}{2}99k(l-x{)}^2$, the latter of which is found by summing the potential energy of both springs (extended from their equilibrium positions) respectively.

$$\begin{array}{rl}L& =T-U\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(\frac{1}{2}k(l-x{)}^2+\frac{1}{2}99k(l+x{)}^2\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\frac{1}{2}k\left((l^2+x^2-2xl)+99(l^2+x^2+2xl)\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\frac{1}{2}k\left(100l^2+100x^2+196xl\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(50k{l}^2+50k{x}^2+98kxl\right)\\ & =\boxed{\frac{1}{2}m{\dot{x}}^2-50k{x}^2-50k{l}^2-98kxl}\end{array}$$

Part C (16 marks)

From this Lagrangian, we can calculate the corresponding Euler-Lagrange equation and hence derive the equation of motion for the point particle. First, the Euler-Lagrange equation by definition is…

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0$$

Hence, if we calculate the required derivatives from the previously found Lagrangian:

$$\begin{array}{rl}& \frac{\partial L}{\partial \dot{x}}=m\dot{x}⟹\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)=m\ddot{x}\\ & \frac{\partial L}{\partial x}=-100kx-98kl\end{array}$$

Then we can substitute them into the aforementioned definition to give the Euler-Lagrange equation:

$$\boxed{m\ddot{x}+100kx+98kl=0}$$

Hence the equation of motion for the system is…

$$\boxed{\ddot{x}=-\frac{100kx+98kl}{m}}$$

Part D (12 marks)

Repeating the previous steps for the case that both spring constant are equal to $50k$, we find that the degrees of freedom are still $\text{d.f.}=1\cdot 1-0=\boxed{1}$ (as there are no new attachments to the particle apart from the springs that can extend infinitely, hence do not count as holonomic contraints, and the dimensions/number of particles are the same), and the Lagrangian is…

$$\begin{array}{rl}L& =T-U\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(\frac{1}{2}50k(l+x{)}^2+\frac{1}{2}50k(l-x{)}^2\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(\frac{1}{2}50k((l+x{)}^2+(l-x{)}^2)\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(\frac{1}{2}50k(l^2+x^2+2xl+l^2+x^2-2xl)\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(\frac{1}{2}50k(2l^2+2x^2)\right)\\ & =\left(\frac{1}{2}m{\dot{x}}^2\right)-\left(50k{l}^2+50k{x}^2\right)\\ & =\boxed{\frac{1}{2}m{\dot{x}}^2-50k{x}^2-50k{l}^2}\end{array}$$

Hence, the Euler-Lagrange equation and equation of motion (respectively) are…

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)-\frac{\partial L}{\partial x}=0⟺\boxed{m\ddot{x}+100kx=0}⟺\boxed{\ddot{x}=-\frac{100kx}{m}}$$

Part E (6 marks)

The first equation, using a $1:99$ spring constant ratio, yielded the equation of motion $\ddot{x}=-\frac{100kx+98kl}{m}$, whilst the second used the ratio $1:1$ and yielded $\ddot{x}=-\frac{100kx}{m}$.

Comparing these results, we find that they’re almost the exact same, but when the ratio between the two spring’s spring constants are $1:1$, then the equation of motion is no longer dependent on $l$, the resting spring length. This is shown by the lack of this variable in the second equation of motion, but presence of the variable in the first.

Physically, this makes sense, as if the springs are equally strong then the system will exhibit more symmetric behaviour, where any forces balance out more uniformly; this contrasts with if the springs have different strengths, where the system will then be sensitive to the initial spring lengths. This might lead to the second system exhibiting simpler harmonic motion, too.

---

Problem 2 (50 total marks)

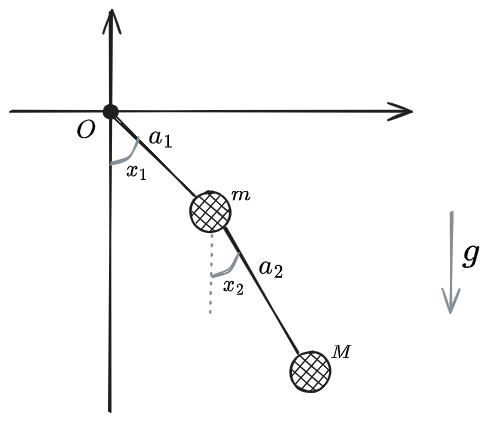
There is a Lagrangian in the following form, where $m,M,a_1,a_2,g$ are constants and $x_1,x_2$ are two generalised coordinates…

$$L=\frac{1}{2}(m+M)a_1^2{\dot{x}}_1^2+\frac{1}{2}M{a}_2^2{\dot{x}}_2^2+M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\cos (x_1-x_2)+(m+M)g{a}_1\cos (x_1)+Mg{a}_2\cos (x_2)$$

My interpretation of this Lagrangian is a double pendulum illustrated below:

Part A (30 marks)

This Lagrangian is dependent on two generalised coordinates (this makes sense, as there are two particles moving in two dimensions with two holonomic constraints - the two massless rigid rods attached to the particles -, since the Lagrangian describes a double pendulum, hence $\text{d.f.}=2\cdot 2-2=2$), so should have two Euler-Lagrange equations defined by the equations:

$$\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{x}}_1}\right)-\frac{\partial L}{\partial x_1}=0\text{and}\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{x}}_2}\right)-\frac{\partial L}{\partial x_2}=0$$

If we evaluate the first equation, then we first need to find the required derivatives. We’ll start with the partial derivatives…

$$\begin{array}{rl}& \frac{\partial L}{\partial {\dot{x}}_1}=(m+M)a_1^2{\dot{x}}_1+M{a}_1{a}_2{\dot{x}}_2\cos (x_1-x_2)\\ & \frac{\partial L}{\partial x_1}=-M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)-(m+M)g{a}_1\sin (x_1)\end{array}$$

Then we can calculate $\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{x}}_1}\right)$, as it’ll involve a bit more work:

$$\begin{array}{rl}\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{x}}_1}\right)& =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2\cdot \left(\frac{d}{dt}({\dot{x}}_2\cos (x_1-x_2))\right)\\ & =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2\cdot \left(\frac{d}{dt}({\dot{x}}_2)\cos (x_1-x_2)+{\dot{x}}_2\frac{d}{dt}(\cos (x_1-x_2))\right)\\ & =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2\cdot \left({\ddot{x}}_2\cos (x_1-x_2)-{\dot{x}}_2({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2)\right)\\ & =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2{\ddot{x}}_2\cos (x_1-x_2)-M{a}_1{a}_2{\dot{x}}_2({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2)\end{array}$$

Which we can then substitute into the original definition and simplify slightly…

$$\begin{array}{rl}0& =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2{\ddot{x}}_2\cos (x_1-x_2)-M{a}_1{a}_2{\dot{x}}_2({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2)+M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)+(m+M)g{a}_1\sin (x_1)\\ & =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2{\ddot{x}}_2\cos (x_1-x_2)-M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)+M{a}_1{a}_2{\dot{x}}_2^2\sin (x_1-x_2)+M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)+(m+M)g{a}_1\sin (x_1)\\ & =(m+M)a_1^2{\ddot{x}}_1+M{a}_1{a}_2{\ddot{x}}_2\cos (x_1-x_2)+M{a}_1{a}_2{\dot{x}}_2^2\sin (x_1-x_2)+(m+M)g{a}_1\sin (x_1)\\ & =a_1((m+M)a_1{\ddot{x}}_1+M{a}_2{\ddot{x}}_2\cos (x_1-x_2)+M{a}_2{\dot{x}}_2^2\sin (x_1-x_2)+(m+M)g\sin (x_1))\end{array}$$

Resulting in the first Euler-Lagrange equation:

$$\boxed{a_1((m+M)a_1{\ddot{x}}_1+M{a}_2{\ddot{x}}_2\cos (x_1-x_2)+M{a}_2{\dot{x}}_2^2\sin (x_1-x_2)+(m+M)g\sin (x_1))=0}$$

Repeating the same steps for the second Euler-Lagrange equation: First, the required derivatives…

$$\begin{array}{rl}& \frac{\partial L}{\partial {\dot{x}}_2}=M{a}_2^2{\dot{x}}_2+M{a}_1{a}_2{\dot{x}}_1\cos (x_1-x_2)\\ & \frac{\partial L}{\partial x_2}=-(-1)M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)-Mg{a}_2\sin (x_2)\end{array}$$ $$\begin{array}{rl}\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{x}}_2}\right)& =\frac{d}{dt}\left(M{a}_2^2{\dot{x}}_2+M{a}_1{a}_2{\dot{x}}_1\cos (x_1-x_2)\right)\\ & =M{a}_2^2{\ddot{x}}_2+M{a}_1{a}_2\left(\frac{d}{dt}({\dot{x}}_1)\cos (x_1-x_2)+{\dot{x}}_1\frac{d}{dt}(\cos (x_1-x_2))\right)\\ & =M{a}_2^2{\ddot{x}}_2+M{a}_1{a}_2\left({\ddot{x}}_1\cos (x_1-x_2)-{\dot{x}}_1({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2)\right)\\ & =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2))\end{array}$$

Then, substituting these values into the original definition:

$$\begin{array}{rl}0& =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2))-M{a}_1{a}_2{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)+Mg{a}_2\sin (x_2)\\ & =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1({\dot{x}}_1-{\dot{x}}_2)\sin (x_1-x_2)-a_1{\dot{x}}_1{\dot{x}}_2\sin (x_1-x_2)+g\sin (x_2))\\ & =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1(({\dot{x}}_1-{\dot{x}}_2)+{\dot{x}}_2)\sin (x_1-x_2)+g\sin (x_2))\\ & =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1^2\sin (x_1-x_2)+g\sin (x_2))\end{array}$$

Hence the second Euler-Lagrange equation is…

$$\boxed{M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1^2\sin (x_1-x_2)+g\sin (x_2))=0}$$

Note: both of these Euler-Lagrange equations could be simplified further by dividing through by $a_1$ and $M{a}_2$ respectively, but as these weren’t explicitly non-zero in the question I simply factorised them out instead to avoid division by zero.

Part B (20 marks)

We now have two Euler-Lagrange equations:

$$\begin{array}{rl}0& =a_1((m+M)a_1{\ddot{x}}_1+M{a}_2{\ddot{x}}_2\cos (x_1-x_2)+M{a}_2{\dot{x}}_2^2\sin (x_1-x_2)+(m+M)g\sin (x_1)),\\ 0& =M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1\cos (x_1-x_2)-a_1{\dot{x}}_1^2\sin (x_1-x_2)+g\sin (x_2)).\end{array}$$

We can then simplify these results assuming that $x_1$ and $x_2$ are small values (less than $0.1\text{ radians}$), such that…

1. $\cos (x_1-x_2)\approx 1$,
2. $\sin (x_1-x_2)\approx x_1-x_2$,
3. $\sin (x_1)\approx x_1$,
4. $\sin (x_2)\approx x_2$.

Hence we can approximate the two Euler-Lagrange equations as…

$$\boxed{\begin{array}{rl}0& \approx a_1((m+M)a_1{\ddot{x}}_1+M{a}_2{\ddot{x}}_2+M{a}_2{\dot{x}}_2^2(x_1-x_2)+(m+M)g(x_1)),\\ 0& \approx M{a}_2(a_2{\ddot{x}}_2+a_1{\ddot{x}}_1-a_1{\dot{x}}_1^2(x_1-x_2)+g{x}_2).\end{array}}$$

Note: we stop here, as the question only asked to simplify, not solve, the coupled second-order nonlinear differential equations.