Coding Theory Coursework

Alternative forms: Coding Theory Coursework.pdf and Coding Theory Coursework.docx.

Problem CW1 (25 total marks)

Consider the code $C\subset {\mathbb{F}}_5^3$ consisting of the following codewords…

$$c_1=243,c_2=321,c_3=102.$$

Part A (10 marks)

First, we can calculate the Hamming distance between each codeword, as follows:

$$\begin{array}{rl}d(c_1,c_2)& =3,\\ d(c_1,c_3)& =3,\\ d(c_2,c_3)& =3\end{array}$$

We can then find the minimal distance $d_{\text{min}}(C)$ of the code $C$ and use it to determine how many errors it can detect/correct with the Definition of Distance Theorem:

Given that $C$ has a minimal distance $\boxed{d_{\text{min}}(C)=3}$,

1. $d_{\text{min}}(C)\ge t+1$, where $t\in \mathbb{N}$, then $C$ detects $t$ errors; hence $3\ge t+1⟹t=\lfloor 3-1\rfloor ⟹\boxed{t=2}$.
2. $d_{\text{min}}(C)\ge 2k+1$, where $k\in \mathbb{N}$, then $C$ corrects $k$ errors; hence $3\ge 2k+1⟹k=\lfloor \frac{3-1}{2}\rfloor ⟹\boxed{k=1}$.

Part B (15 marks)

To find all the words in ${\mathbb{F}}_5^3$ which follow the two constraints:

1. Their first symbol is equal to $0$,
2. They have a Hamming distance of exactly $3$ from every codeword of $C$ simultaneously, i.e. their second symbol isn’t $0$, $2$, or $4$, and their third symbol isn’t $1$, $2$, or $3$.

We can first list all the words which meet the first constraint:

$$\{000,001,002,003,004,010,011,012,013,014,020,021,\dots ,044\}:16\text{ total}$$

And then filter them by the second constraint:

$$\boxed{\{010,014,030,034\}}:4\text{ total}$$

---

Problem CW2 (10 marks)

Consider the code $C=\{0000,1111,0101,1010\}\subset {\mathbb{F}}_2^4$ in a symmetric channel with symbol error probability $p=0.05$ Suppose the codeword $0000$ is sent and is received with exactly one erroneous symbol.

We can find the probability of this occurring by determining the ways that it can happen, $\left(\genfrac{}{}{0ex}{}{4}{1}\right)=4$, and then multiplying this by the probability of each symbol being as we want: one symbol being erroneous, $p$, and three symbols being correct, $(1-p{)}^3$…

$$\begin{array}{rl}P(\text{one erroneous symbol})& =4\cdot p\cdot (1-p{)}^3\\ & =4\cdot 0.05\cdot (1-0.05{)}^3\\ & =0.2\cdot (0.95{)}^3\\ & =0.2\cdot 0.857375\\ & =0.171475\\ & =\boxed{17.1475\%}\end{array}$$

---

Problem CW3 (35 total marks)

The following code is built to encode certain special moves of a prominent videogame as a combination of inputs from a controller…

$$C=\{\downarrow \searrow \to p,\to \downarrow \to p,\downarrow \swarrow \leftarrow k,p\to kp\}$$

Part A (5 marks)

We can draw a graph where the elements of $C$ are represented by vertices which are only connected by an edge if (and only if) their Hamming distance is exactly one:

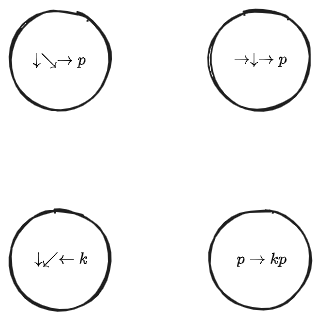
With this graph, we can count how many edges there are and hence how many elements have a Hamming distance of exactly one. However, there are no pairs of elements with a Hamming distance of exactly one, the minimum is two between $\downarrow \searrow \to p$ and $\to \downarrow \to p$.

Part B (10 marks)

The four parameters of $C$ are:

• $\boxed{n=4}$,
• $\boxed{M=4}$,
• $\boxed{d=2}$,
• $\boxed{q=7}\because A=\{\leftarrow ,\swarrow ,\downarrow ,\searrow ,\to ,k,p\}$.

Part C (10 marks)

To determine how many errors $C$ can detect and correct we can use the Definition of Distance Theorem:

Given that $C$ has a minimal distance $d_{\text{min}}(C)=2$ (found in the previous part),

1. $d_{\text{min}}(C)\ge t+1$, where $t\in \mathbb{N}$, then $C$ detects $t$ errors; hence $2\ge t+1⟹t=\lfloor 2-1\rfloor ⟹\boxed{t=1}$.
2. $d_{\text{min}}(C)\ge 2k+1$, where $k\in \mathbb{N}$, then $C$ corrects $k$ errors; hence $2\ge 2k+1⟹k=\lfloor \frac{2-1}{2}\rfloor ⟹\boxed{k=0}$.

Part D (10 marks)

Given a space of words of length four, over the alphabet used to build $C$, we can calculate the volume of a solid sphere of radius $2$ and centre $\downarrow \searrow \to p$, i.e. $S_2(\downarrow \searrow \to p)$, by using the Definition of the Volume of a Solid Hamming Distance Sphere:

$$\begin{array}{rl}|S_2(\downarrow \searrow \to p)|& =\sum _{i=0}^2\left(\genfrac{}{}{0ex}{}{4}{i}\right)(7-1{)}^i\\ & =\sum _{i=0}^2\left(\genfrac{}{}{0ex}{}{4}{i}\right)\cdot 6^i\\ & =\left(\genfrac{}{}{0ex}{}{4}{0}\right)\cdot 6^0+\left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot 6^1+\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 6^2\\ & =1\cdot 1+4\cdot 6+6\cdot 6^2\\ & =1+24+216\\ & =\boxed{241}\end{array}$$

Practically, this represents the number of words with Hamming distance 2 from the word $\downarrow \searrow \to p$.

---

Problem CW4 (30 total marks)

The following table lists all codewords of the original code proposed by R. Hamming:

$$\begin{array}{rl}C=\{& 0000000,0001111,0010011,0011100,0100101,0101010,0110110,\dots \\ & 0111001,1000110,1001001,1010101,1011010,1100011,1101100,\dots \\ & 1110000,1111111\}\end{array}$$

Part A (15 marks)

We can prove that Hamming’s original code is perfect by using the Definition of a Perfect Code in Coding Theory:

If this holds…

$$M=\frac{q^n}{\text{vol}(S_{ϵ(d)}(c))}:ϵ(d)=\lfloor \frac{d-1}{2}\rfloor ,\text{for some codeword }c\in C$$

Then the code is perfect. Hence, using the Definition of the Volume of a Solid Hamming Distance Sphere and given that the parameters of Hamming’s original code are $n=7,M=16,d=3,q=2$,

$$\begin{array}{rl}ϵ(d)=\lfloor \frac{3-1}{2}\rfloor =1⟹16& =\frac{2^7}{\text{vol}(S_1(c))}\\ & =\frac{2^7}{\left(\genfrac{}{}{0ex}{}{7}{0}\right)(2-1{)}^0+(\genfrac{}{}{0ex}{}{7}{1})(2-1{)}^1}\text{ by definition}\\ & =\frac{2^7}{1+7}\\ & =\frac{2^7}{2^3}\\ & =2^4\\ & =16\square \end{array}$$

Part B (15 marks)

Suppose that some codeword of Hamming’s original code was sent, but the word $w=0000110$ was received.

The code can reliable correct one erroneous symbol using the nearest neighbour decoding strategy, but if we assume there are two errors in transmission then issues arise since multiple codewords can be Hamming equidistant.

For the word $w$, the following all have a Hamming distance of two:

• $0000000$,
• $0001111$,
• $0110110$.

Hence, there is a $\frac{1}{3}$ chance that the code corrects to the original codeword, and a $\frac{2}{3}$ chance that it doesn’t.