MTH2004 Differential Equations Cheat Sheet

MTH2004 Differential Equations - Cheat Sheet

Made by William Fayers :)

Make sure to read this before the exam - I recommend completing a practice test with it so you learn where everything is and can ask if you don’t understand something. I might’ve made mistakes! There’s a sudoku at the end in case you finish early, and the cheat sheet is generated based on analysis of past exams and given material.

Small warning: the following makes the most sense if you read it all first. It also assumes you have knowledge from the linear algebra module (namely solving simultaneous equations and finding a determinant) - make sure you know this!

Possible Question Topics and their Explanations

0. Useful “Known” Facts

$$\int \ln x=x\ln x+x+c\text{(integral of a natural logarithm)}$$ $$\int (u)dv=uv-\int (v)du\text{(integration by parts)}$$ $$\begin{array}{r}\text{Existence and Uniqueness Theorem: }f(x,y),\frac{\partial f}{\partial y}\text{ are continuous in a region}\\ ⟹\text{unique solution throughout that region, subject to initial conditions.}\end{array}$$ $$\begin{array}{rl}& \text{odd functions: }f(-x)=-f(x)\text{(rotational symmetry)}\\ & \text{even functions: }f(-x)=f(x)\text{(reflective symmetry)}\end{array}$$ $$\text{a point of discontinuity is modelled as the average of its left/right limits}$$

1. Classification of Differential Equations

Given that it’s fully simplified…

1. Order: The highest derivative present in the equation.
   1. Example: $\frac{d^{2}y}{d{x}^2}+3\frac{dy}{dx}+2y=0$ is a second-order DE.
2. Linearity:
   1. Linear: Can be expressed in the form $a_n(x)y^{(n)}+a_{n-1}(x)y^{(n-1)}+\dots +a_1(x)y^{\prime }+a_0(x)y=g(x)$.
   2. Non-linear: Contains products (or powers) of the function, or its derivatives.
3. Constant vs. Non-Constant Coefficients:
   1. Constant: Coefficients of the DE are constants, e.g. $y^{\prime \prime }+3y^{\prime }+4y=0$.
   2. Cauchy-Euler: Coefficients of the DE aren’t constant and are in the form $a{x}^2{y}^{\prime \prime }+bx{y}^{\prime }+cy=0$.
4. Ordinary vs. Partial:
   1. Ordinary Differential Equations (ODEs): Involves functions of a single variable and their derivatives.
   2. Partial Differential Equations (PDEs): Involves functions of multiple variables and their partial derivatives - see section 4.
5. Homogeneous vs. Non-Homogeneous:
   1. Homogeneous: $g(x)=0$.
   2. Non-Homogeneous: $g(x)\ne 0$.
6. Autonomous vs. Non-Autonomous:
   1. Autonomous: Slope function, e.g. $\frac{dy}{dx}$, does not rely on the independent variable, i.e. $\frac{dy}{dx}=f(y)$.
   2. Non-Autonomous: Slope function, e.g. $\frac{dy}{dx}$, relies on the independent variable, i.e. $\frac{dy}{dx}=f(x,y)$, for example relying on time.

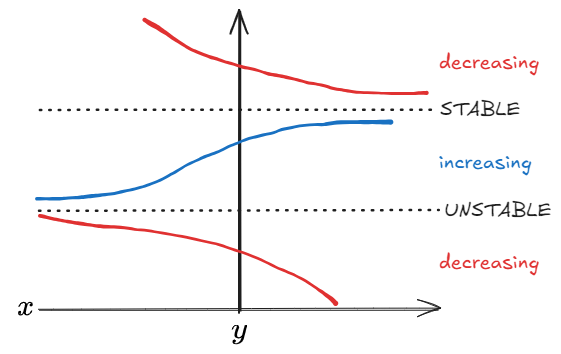
2. Critical Points

1. Finding Critical Points:
   1. Set the first derivative $\frac{dy}{dx}=0$ and solve for $x$.
2. Stability:
   1. Stable: If $\frac{dy}{dx}$ changes from positive to negative, or $\frac{d^{2}y}{d{x}^2}<0$, or two trajectories on a phase portrait go towards the critical point.
   2. Unstable: If $\frac{dy}{dx}$ changes from negative to positive, or $\frac{d^{2}y}{d{x}^2}>0$, or two trajectories on a phase portrait go away from the critical point.
3. Phase Portrait:
   1. Definition: Graphical representation of trajectories to help find stability of critical points.
   2. Method:
      1. Divide the $xy$-plane into regions separated by the critical points, e.g. for $\frac{dy}{dx}=y(a-bx)$ then three regions: $(-\infty ,0)$, $(0,\frac{a}{b})$, and $(\frac{a}{b},\infty )$.
      2. Declare each region as increasing or decreasing, i.e. $\frac{dy}{dx}<0$ is decreasing and $\frac{dy}{dx}>0$ is increasing.
      3. The phase diagram then represents this graphically: arbitrary curves going up or down in each region. These are asymptotic towards the critical points (since the critical points are neither increasing or decreasing by definition).

3. Solving Differential Equations

1. Representing Solutions:
   1. Can use a direction graph to represent a family of solutions, e.g. $y=x+c$.
   2. Plot trivial solution, $c=0$, then plot other values of $c$ as arrows.
2. Exact Solutions:
   1. Use boundary values (conditions) at specific points, i.e. $y(a)=b$.
   2. Substitute in each variable and solve for parameters, e.g. $c,c_1,c_2,...$.
3. First-Order Solutions:
   1. If in the form $\frac{dy}{dx}+P(x)y=Q(x)$ (standard form)…
      1. Find integrating factor $\mu (x)=e^{\int P(x)dx}$.
      2. Multiply equation by integrating factor, then simplify to $\frac{d}{dx}(y\mu (x))=Q(x)\mu (x)$ using the concept of reverse derivatives.
      3. Integrate both sides, then solve for $y$.
   2. If separable (in the form $\frac{dy}{dx}=g(x)h(y)$)…
      1. Rearrange to isolate each variable, i.e. $\frac{1}{g(y)}dy=f(x)dx$ which is equivalent to $\int \frac{1}{g(y)}dy=\int f(x)dx$.
4. Second-Order Solutions:
   1. Given the form $a(x)\frac{d^{2}x}{d{y}^2}+b(x)\frac{dy}{dx}+c(x)y=f(x)$, then the solution $y=y_c+y_p$ (the sum of the complementary function and particular function).
      1. The complimentary function, $y_c$, focuses on the left side of the equation (ignoring constants of integration until the end)…
         1. By assuming a solution for $y$ and substituting into the original equation, we find the characteristic equation (normally in the form of a quadratic, like $a{k}^2+bk+c=0$).
            1. For $a(x)=a$, $b(x)=b$, and $c(x)=c$, assume $y=e^{kx}:y^{\prime }=k{e}^{kx},y^{\prime \prime }=k^2{e}^{kx}$.
            2. For $a(x)=a{x}^2$, $b(x)=bx$, and $c(x)=c$, assume $y=x^m:y^{\prime }=m{x}^{m-1},y^{\prime \prime }=m(m-1)x^{m-2}$.
         2. After simplifying, given that $e^{kx}$ and $x^m$ cannot be $0$, solve the resulting quadratic for $x$ or $m$.
            1. If there’s a repeated solution, we can use reduction of order to find $y_2$. In short, $y_2=y_1\int \frac{e^{-\int \frac{b(x)}{a(x)}dx}}{y_1^2}dx$, i.e…
               1. … if $y_1=e^{kx}$, then $y_2=x{e}^{kx}$.
               2. … if $y_1=x^m$, then $y_2=x^m\ln x$.
            2. If there are complex conjugate solutions, we can use Euler’s formula to get $y_c$ straightaway (skip superposition step): \begin{align*}e^{kx}&= e^{(\alpha\pm i\beta)x}\\&= e^{\alpha x}e^{i\beta x}:e^{i\beta x}=\cos (\beta x)+i\sin (\beta x)\quad\text{(Euler's formula)}\\&= e^{\alpha x}(\cos (\beta x)+i\sin (\beta x))\\&=e^{\alpha x}(C_{1}\cos(\beta x)+C_{2}\sin(\beta x))\quad\text{(adding in constants)}\end{align*}
         3. Using the principle of superposition (the sum of solutions is another solution), find $y_c=C_1{y}_1+C_2{y}_2$, where $C_n$ are the constants of integration previously ignored.
         4. This general solution can contain transient terms - those that will eventually decay to zero as time progresses.
      2. The particular solution, $y_p$, focuses on the right side of the equation, such that $y^{\prime \prime }$ has a coefficient of $1$ (standard form)…
         1. Trivial: If $\text{RHS}=0$, $y_p=0$.
         2. Simple: If $\text{RHS}$ is in the form of a polynomial ($A{x}^n+B{x}^{n-1}+\dots +Cx+D$), exponential ($A{e}^{kx}$), sine/cosine ($A\sin (kx)+B\cos (kx)$), or a combination of these, use undetermined coefficients…
            1. Assume $y_p$ to have the same generic form. Multiply terms by $x$ if they’re multiples of terms in the original equation, to ensure linear independence.
            2. Differentiate the assumed $y_p$ to give $y^{\prime }$ and $y^{\prime \prime }$ to substitute into $\text{LHS}$.
            3. Compare against the assumed $y_p$, equating coefficients to make a system of equations.
            4. Solve the system using Gauss-Jordan elimination, or another method.
         3. Non-Periodic: If $\text{RHS}$ is in a more complicated form and non-periodic, use variation of parameters…
            1. Find the Wronskian $W=W(y_1,y_2)=y_1{y}_2^{\prime }-y_2{y}_1^{\prime }$, where $y_1,y_2$ are from the complementary function.
            2. Find the variable parameters, $u_1=-\int \frac{y_{2}f(x)}{W}$ and $u_2=\int \frac{y_{1}f(x)}{W}$, given that $f(x)=\text{RHS}$.
            3. Find the linear combination of variable parameters and complementary solutions, $y_p=u_1{y}_1+u_2{y}_2$.
         4. Periodic: If $\text{RHS}$ is in a more complicated form and periodic, use a Fourier series:
            1. For $f(x)=\text{RHS}$ defined on $[-L,L]$, $\text{RHS}$ can be transformed into periodic functions depending on its symmetry:
               1. Even function: $f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }{a}_n\cos \frac{n\pi x}{L}$, where $a_n=\frac{2}{L}{\int }_0^{L}f(x)\cos \frac{n\pi x}{L}dx$.
               2. Odd function: $f(x)=\sum _{n=1}^{\infty }{b}_n\sin \frac{n\pi x}{L}$, where $b_n=\frac{2}{L}{\int }_0^{L}f(x)\sin \frac{n\pi x}{L}dx$.
               3. Neither: Sum as if it is even and odd, modifying the integrals to evaluate $[-L,L]$, rather than doubling $[0,L]$, since there’s no symmetry.
            2. Find the solution as with a “simple sine/cosine” with undetermined coefficients.
         5. Infinite Non-Periodic Functions:
            1. Fourier Integrals: Defined as $f(x)={\int }_{-\infty }^{\infty }F(k)e^{ikx}dk$, where $F(k)$ is the Fourier transform of $f(x)$.
            2. Fourier Transform: The Fourier transform of a function $f(x)$ is given by: $F(k)={\int }_{-\infty }^{\infty }f(x)e^{-ikx}dx$, where the inverse Fourier transform is: $f(x)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(k)e^{ikx}dk$. Useful for transforming things into the frequency domain and back to the spatial domain - sometimes used when solving PDEs since they convert into ODEs.
               1. Properties:
                  • Linearity: $F(af(x)+bg(x))=aF(f)+bF(g)$ allows for the superposition of solutions.
                  • Time Shifting: $F(f(x-a))=e^{-ika}F(k)$ helps in analyzing shifted functions.
                  • Frequency Shifting: $F(e^{iax}f(x))=F(k-a)$ is useful for modulation in signal processing.
                  • Scaling: $F(f(ax))=\frac{1}{|a|}F\left(\frac{k}{a}\right)$ aids in understanding how scaling affects frequency components.
            3. Fourier Convolution: The convolution of two functions $f$ and $g$ is defined as: $(f\ast g)(x)={\int }_{-\infty }^{\infty }f(t)g(x-t)dt$.
               1. Convolution Theorem: The Fourier transform of the convolution of two functions is the product of their Fourier transforms: $F(f\ast g)=F(f)\cdot F(g)$.
               2. Properties:
                  • Commutative: $f\ast g=g\ast f$ indicates that the order of convolution does not matter.
                  • Associative: $f\ast (g\ast h)=(f\ast g)\ast h$ shows that convolution can be grouped in any way.
                  • Distributive: $f\ast (g+h)=f\ast g+f\ast h$ allows for the distribution of convolution over addition.

4. Partial Differential Equations (PDEs)

1. Classification:
   1. Linearity: Can be expressed in the form $a(x,y)\frac{{\partial }^{2}u}{\partial x^2}+b(x,y)\frac{{\partial }^{2}u}{\partial y^2}+c(x,y)\frac{\partial u}{\partial x}+d(x,y)\frac{\partial u}{\partial y}+e(x,y)u=f(x,y)$, and hence doesn’t contain products/powers of the function or its derivatives.
   2. Order: The highest order of derivative in the equation, e.g. $\frac{{\partial }^{2}u}{\partial y^2}-c^2\frac{{\partial }^{2}u}{\partial x^2}=0$ is a second-order PDE.
   3. Type:
      1. Given the standard linear form, calculate the discriminant $\Delta =B^2-4AC$, where $A=a(x,y),B=b(x,y),C=c(x,y)$.
      2. If the discriminant $\Delta$ is…
         1. less than zero, it’s elliptic.
         2. equal to zero, it’s parabolic.
         3. greater than zero, it’s hyperbolic.
2. Solving:
   1. Assume the solution $u(x,t)=X(x)T(t)$ ($t$ could also be $y$, or something else depending on context), then substitute into the PDE.
   2. Re-arrange to get terms involving $X$ on one side and terms involving $Y$ on the other.
   3. Set each side equal to a constant (often denoted as $-\lambda$, a separation constant) to get two ODEs, which can then be solved.
   4. These two solutions are $X(x)$ and $T(t)$, which can then be substituted back into the assumed solution $u(x,t)$.

Sudoku